Mixture of Experts

Introduction

Mixture of Experts (MoE) is a method for dividing complex tasks into smaller, more manageable segments. The MoE approach originated in the domain of speech signal classification. Initially, it was developed to classify phonemes in speech signals from different speakers, employing multiple "expert" networks, each focusing on specific aspects of the problem. Over time, MoE has evolved to the form used with Large Language Models (LLMs), enabling it to handle diverse and complex tasks more efficiently.

Fundamental Components of MoE

The MoE framework is built on a few fundamental components:

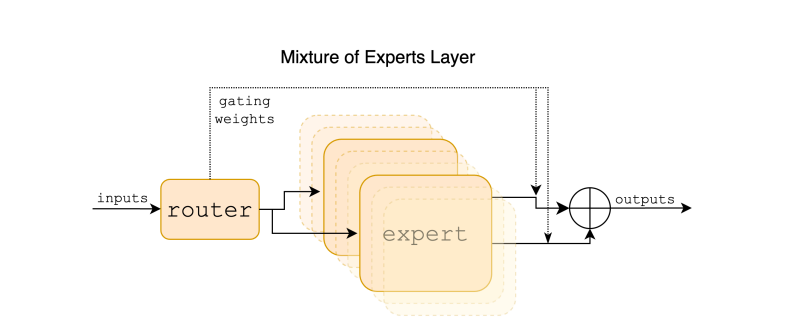
1. Experts: These specialized models or networks are trained for specific parts of a problem. All experts receive the same input, but their outputs vary based on their specialized training.
2. Gating Function: Acting as a decision-maker, this function routes inputs to appropriate experts and assigns dynamic weights to each expert's output, influencing the final combined output. The gating function often employs a network with a softmax function.
3. Combined Output: Outputs from the experts are merged based on the gating function's weights, creating a cohesive final output. This combination can be achieved through methods like selecting the expert with the highest output or using a weighted sum prediction.

Advanced Concepts and Structures in MoE

The MoE framework has been applied to neural network architectures such as transformers using more advanced structures.

1. Hierarchical MoE: Incorporating multiple gating levels in a tree structure, similar to decision trees, allows for complex and nuanced decision-making. Each gating level can focus on different input data aspects.
2. Switch Transformers: A notable advancement in MoE, Switch Transformers streamline the routing process with concepts like top-k gating. They introduce mechanisms for load balancing to ensure even distribution of computational load among experts.
3. GShard Implementation: GShard modifies transformers by replacing alternate FFN layers with MoE layers, using top-2 gating. This design benefits large-scale computing and helps maintain efficiency and balanced load at scale, as depicted here:

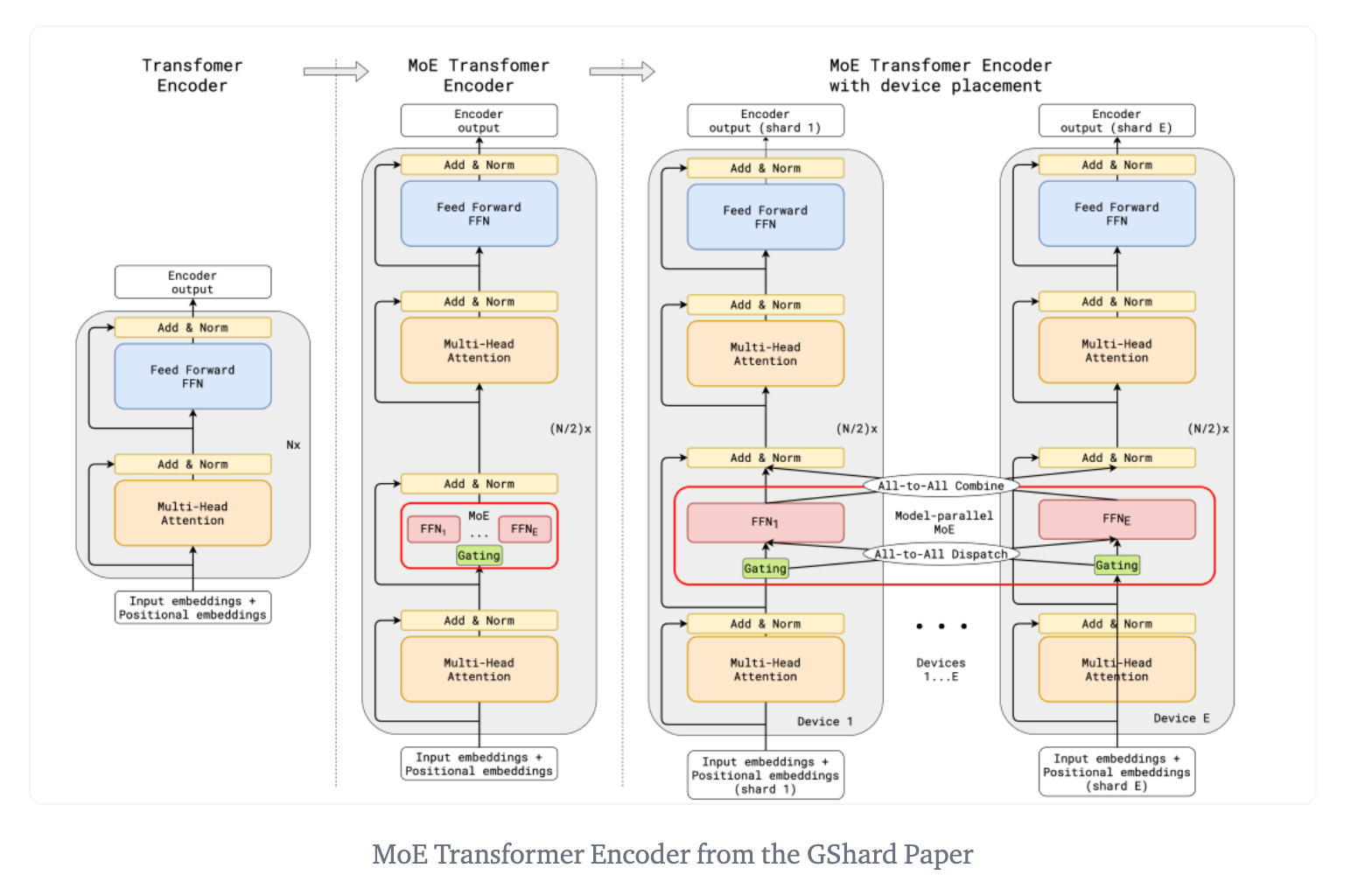
4. Expert and Parameter Capacity: The concept of expert capacity in MoE architectures sets a threshold for the amount of input an expert can process. This is crucial for resource management and preventing certain experts from becoming overloaded.
5. Selective Precision: This approach uses different precision levels for different model parts. For instance, training experts with lower precision while using full precision for the rest of the computations helps reduce costs and memory usage.
6. Router Z-Loss: Introduced to stabilize the training of sparse models without quality degradation, Router Z-Loss penalizes large logits entering the gating network, reducing roundoff errors significant in exponential functions like gating.
7. Specialization of Experts: In encoder-decoder setups, encoder experts often specialize in groups of tokens or concepts, while decoder experts show less specialization. This can be influenced by routing and load balancing strategies.
8. Adaptive Mixtures of Local Experts: Using a gaussian mixture model, each expert predicts a gaussian distribution, with the weighting function typically being a linear-softmax function. The model is trained by maximizing likelihood estimation.

These structures and concepts highlight MoE architectures' flexibility and adaptability, making them powerful for handling complex and large-scale machine learning challenges.

Case Study: Mixtral

The Mixtral 8x7B model from Mistral.ai is an advanced implementation of the Sparse Mixture of Experts (SMoE) methodology in language models:

This architecture is characterized by several key features and performance metrics

Mixtral Architecture and Design

• Experts Configuration: Each layer of Mixtral 8x7B comprises 8 feedforward blocks (referred to as experts).
• Router Network: A crucial component in this architecture is the router network. For every token and at each layer, this network selects two experts to process the current token and then combines their outputs. This dynamic selection means that the experts engaged can vary at each timestep.
• Parameter Utilization: Despite having access to a large parameter set (46.7 billion parameters in total), Mixtral utilizes only 12.9 billion active parameters during inference for each token. This efficient use of parameters allows the model to achieve the speed and cost of a 12.9 billion parameter model, while harnessing the power of a much larger model.

Mixtral Performance and Capabilities

• Language Support: Mixtral 8x7B effectively handles multiple languages, including English, French, Italian, German, and Spanish.
• Context Handling: The model can gracefully manage a context of up to 32,000 tokens.
• Application Domains: It shows remarkable performance in areas like code generation and multilingual tasks.
• Benchmark Performance: When compared to other models such as Llama 2 70B and GPT-3.5, Mixtral 8x7B either matches or outperforms them across various benchmarks. It is particularly strong in mathematics and code generation benchmarks.
• Instructed Models: There is also a version of Mixtral 8x7B, called Mixtral 8x7B - Instruct, optimized through fine-tuning for following instructions, achieving high scores on benchmarks like MT-Bench.

Mixtral Deployment and Usage

• Open-Source and Licensing: Mixtral is released under the Apache 2.0 license, contributing to the open model community and fostering new developments in AI.
• Integration with Open-Source Platforms: Efforts have been made to integrate Mixtral with open-source deployment stacks like vLLM, which includes efficient inference kernels.

Deployment considerations

Deploying MoE models presents several challenges, particularly in terms of hardware requirements and the complexities involved in training and fine-tuning. However, recent advancements and strategies are addressing these issues effectively.

Challenges

Load Balancing and Efficient Training: One of the main challenges in training MoE models is ensuring efficient load balancing. This involves the distribution of tasks among experts to prevent overloading a few while underutilizing others. Traditional MoE training often leads to certain experts being favored over others, necessitating mechanisms to ensure all experts are equally important. Implementing auxiliary loss functions can mitigate this by encouraging a more even distribution of training examples among all experts.

Expert Parallelism and Memory Consumption: MoE models, despite requiring less computation than traditional transformer models, tend to increase memory usage significantly. This is due to the additional feed-forward networks (FFNs) introduced by the expert layers. To manage this, strategies like expert parallelism, where the MoE layers are distributed across multiple devices, can be employed. However, this approach increases communication requirements among devices hosting different experts, potentially impacting training and deployment efficiency.

Solutions

Expert Offloading: This is process of offloading entire experts (i.e., subsets of the model specialized in certain tasks or types of data) to different hardware resources. In large-scale MoE models, not all experts need to be active for every input. Expert offloading involves dynamically deciding which experts to run and where to run them (e.g., on different CPUs, GPUs, or even separate machines in a distributed computing environment). This approach helps in managing computational resources more efficiently by only utilizing the necessary experts for a given task and can be crucial in scenarios where the model is too large to fit into a single machine's memory or processing capacity.

Parameter Offloading: This technique is beneficial for managing large models with limited accelerator memory. It works by dynamically loading model parameters as needed for computation, which is particularly effective for large-batch data processing. This technique can be slower for interactive tasks like chat assistants, as these require processing fewer tokens at a time, leading to delays in loading the next layer's parameters. Despite these challenges, the technique opens new avenues for efficient utilization of MoE models in language processing tasks on desktop or low-end cloud instances.

Parameter Efficiency: Recent innovations have introduced more parameter-efficient MoE frameworks. For instance, using lightweight “adapters” as experts on top of a pretrained dense model can significantly reduce memory requirements during both training and inference. This approach freezes most parameters during training, reducing computational overhead and memory requirements for storing optimizer states. At inference, this structural modularity translates to significant memory savings, as only a single copy of the model backbone and lightweight experts need to be stored.

Optimized Routing and Capacity Management: Modern MoE models, such as Switch Transformers, use strategies like simplified single-expert routing and optimized expert capacity management. These approaches help reduce router computation, batch sizes for each expert, and communication costs. Expert capacity management, in particular, involves setting a threshold for the number of tokens each expert can process, which helps to balance computational resources.

Innovative Training Techniques: The training of MoE models has seen significant improvements with techniques like selective precision. This involves training experts at lower precision levels, reducing computation and memory requirements without degrading model quality. Such approaches can lead to more stable training, especially when combined with high-precision routing computations.

Applications

MoE models are being applied in various real-world scenarios, showcasing their versatility and effectiveness in different domains. Here are some notable applications and case studies:

Multi-Task Learning in Computer Vision: In the field of computer vision, MoE models have been innovatively applied to multi-task learning. A notable example is Mod-Squad, a model that integrates MoE layers into a transformer model for optimization in multi-task learning scenarios. This approach formalizes the cooperation and specialization processes by matching experts and tasks during training. This structure allows for sharing some parameters among related tasks while enabling specialization for specific data types or tasks. This results in a model that is adaptable and scalable, particularly when dealing with a large number of tasks and varying training set sizes.

Graph Neural Networks: MoE models have also found applications in graph neural networks (GNNs), especially in dealing with large-scale graphs with diverse structures. The Graph Mixture of Experts (GMoE) model, for instance, allows individual nodes in a graph to dynamically select information aggregation experts. These experts are trained to capture distinct subgroups of graph structures, enhancing the generalization capacity of GNNs. This approach is beneficial for a variety of tasks, including graph, node, and link prediction, as it manages to balance diversity and computational efficiency effectively.

Future Directions

MoE models are improving in computational efficiency and training methodologies. Here are some key areas of ongoing research and development:

Improving Computational Efficiency: This area of research seeks to merge the functionalities of multiple experts into one framework to improve computational efficiency. This involves optimizing the usage of floating-point operations (FLOPs) and managing the complexity of the models. The aim is to achieve better performance without significantly increasing the computational resources required. This approach also includes exploring efficient gating mechanisms that can select the appropriate expert for a given input more effectively.

Expert Specialization with Regularization: Another area is the specialization of experts within the MoE models. Traditionally, MoE training does not promote an equitable distribution of samples among experts. Recent studies are exploring the use of auxiliary losses as regularization to enhance the distribution process. This approach aims to balance the workload among experts more effectively.

Attentive Gating Mechanisms: The development of novel gating architectures, such as attentive gates, is also underway. These attentive gates can focus on different aspects of the input and target data, thereby enabling the gate to learn better segmentation and assign tasks to different experts more efficiently. This innovation aims to improve task distribution and expert utilization capabilities.

Information Theoretic Performance Metrics: New metrics are being introduced to better evaluate the performance of MoE models. These metrics aim to measure gating sparsity and expert utilization more effectively. They help in understanding how well the gate distributes samples to experts and how efficiently it utilizes the experts.

MoE architectures provide a way to build more efficient, scalable, and specialized AI models that can better handle the complexity and diversity of real-world tasks and datasets. They are a step towards creating AI systems that can adapt and excel in a wide range of applications.